针对文件的编解码操作
这一小节,我们将对一副图片进行网络编码操作,并对其进行解码操作,将一副图片编码成个小文件,再将这个文件进行还原,还原之后,该图片能够正常打开。需要注意的是,我们在这个编解码过程中,并没有依赖于真实的网络,仅是在数学上对其进行计算,网络拓扑的特点决定了其数据包的再编码方式,我们将通过一个转移矩阵来体现网络特点。在真实的世界里,网络编码的核心操作,也的确就是这样的。
对于文件的编解码操作的应用其实非常广泛,不光网络编码领域用到,传统的分布式存储领域,也广泛地用到。比如运营商将用户上传的文件分片,编码,然后存储在多台服务器的集群中,实现冗余存储,即使网络中的个别存储服务器发生故障,仍然能够恢复出数据。
我先简单介绍介绍一下流程,然后再具体地介绍每个部分的设计细节。
- 通过
fopen读取获得待读入文件的句柄; - 获得文件大小;将其平均分为个切片,无法整除的时候补零,此时每个切片的长度记为;
- new一个二维数组,尺寸;
- 随机生成一个的生成矩阵;
- 再new一个二维数组,尺寸仍为;
- 计算,这样便可以获得编码后的数据,矩阵的每一行都表示一个编码后的数据。由于我们上一步为分配空间的时候,多分配了个字节。我们需要将中对应的维向量保存进去;
- 之后,通过
fwrite将矩阵的每一行分别输出至硬盘,形成个小文件,后缀名任意; - 第二步,我们需要对其中的几个文件进行再次的线性混合,这个操作,其实就是模拟文件在网络的中间节点经过线性混合后的情景。
- 随机选择其中的几个文件,比如3个文件,将这三个文件的数据读入一个的矩阵。
- 再随机生成一个的二维矩阵作为再编码矩阵,用这个矩阵左乘上一步的,得到再编码后的数据,最后,将再编码后的3个数据分片用
fwirte重新输出到硬盘.此过程中不必对再编码矩阵做保存和处理。 - 最后一步就是解码了。随机将个编码后的文件(包括经过再编码的)从硬盘读入一个的二维数组,再new一个二维数组,用来保存系数,系数我们之前保存在中了。
- 首先判断系数矩阵是否满秩,采用随机线性网络编码,当在这个有限域时,大约有0.996的概率能保证其是满秩的。由于不是100%的概率,我们必须要check他的可解码性。解码的条件就是判断系数矩阵是不是满秩的。
- 当满秩时,在求得逆矩阵;
- 最后,用乘以第9步中的矩阵,即可恢复出原始数据了。
下面介绍程序的各部分功能并给出主要代码。
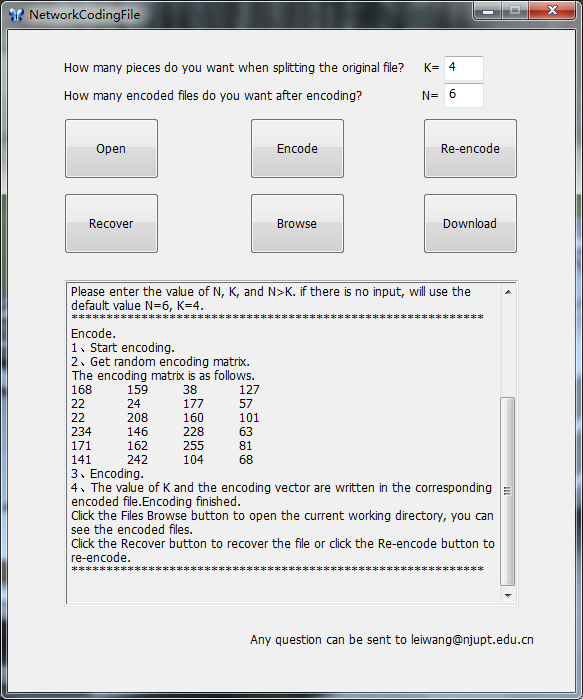
这是程序执行时的界面图,介绍下各部分的功能:
1、值、值。文件进行编码前需要把文件平均分成部分,编码生成的编码文件的个数就是 值。这两个值用户可以输入,且,如果没有输入,默认值。

2、Open按钮。点击后可以在电脑中选择一个你想要编码的文件。

3、Encode按钮。点击开始编码,它的功能分为①把文件读入数组,②生成随机编码矩阵,③用编码矩阵乘以文件数据矩阵,完成编码,④把K值,编码矩阵和编码结果组合成一个矩阵分开写入N个encodeFile.nc文件。
4、Re-encode按钮。点击选择多个encodeFile文件进行再编码。执行过程分为①打开文件选择界面多选文件,②生成随机在编码矩阵,③把文件写入二维数组,④用编码矩阵乘以文件数据矩阵,完成编码,⑤把再编码后的数据写回文件,对文件重命名为re_encodeFile.nc文件。
5、Recover按钮。点击实现解码恢复原文件。执行过程分为①打开文件选择界面多选文件。②如果选择的文件数目不够,会提示至少需要选择几个文件,点击Recover重新选择文件。③把文件读入数组,并从中分离编码矩阵和编码结果。④对编码矩阵求逆,并用逆矩阵乘以编码结果,实现解码。⑤把解码数据写入recovery文件。至此恢复文件完成,程序的核心任务已经完成。

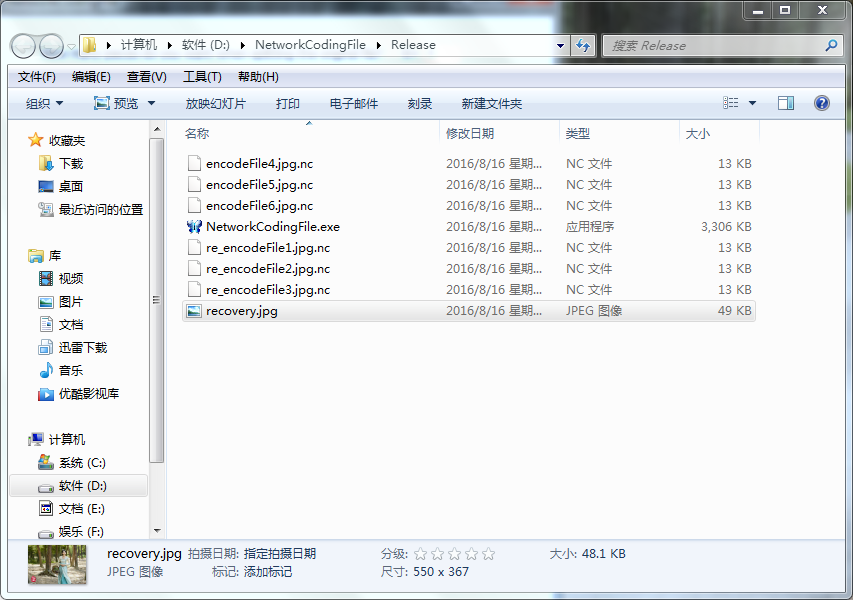
6、Browse按钮。点击Browse按钮可以打开当前工作目录,方便查看执行过程中生成的编码文件encodefile、再编码文件re_encodefile和恢复出来的recovery文件。
7、Download按钮。点击后跳转到github网站下载源代码。 8、最下面的edit control框。用来显示程序执行的步骤,并对程序的使用进行必要的提示。 9、为了方便下次选择.nc文件,在再次点击Encode按钮和关闭程序时,都会自动删除程序执行过程中生成的.nc文件,解码结果recovery文件不会被删除。
接下来给出几个操作中的核心代码。 1、选择文件。打开文件选择器,从本地选择你想编码的文件。
CFileDialog opendlg(TRUE, _T("*"), _T("*"), OFN_OVERWRITEPROMPT, _T("所有文件(*.*;)|*.*||"), NULL);//选择文件
if (opendlg.DoModal() == IDOK) //把文件地址赋给CString类型的g_filePath
{
g_filePath = opendlg.GetPathName();
}
2、编码前把文件读入数组的操作。
g_extName = g_filePath.Right(g_filePath.GetLength() - g_filePath.ReverseFind('.') - 1);//获取文件的扩展名
USES_CONVERSION;
char* pfilename = T2A(g_filePath); //类型的转换Cstring转换为char*
FILE* fp;
fopen_s(&fp, pfilename, "rb"));
fseek(fp, 0, SEEK_END); //文件指针移到文件末尾
long nSize = ftell(fp); //获取文件的总长
long nLen = nSize / K + (nSize % K != 0 ? 1 : 0); //把文件平均分成K份,每份长度为nLen个字节
byte* buffer = new byte[K*nLen]; //使用buffer一维数组转存到二维数组
for (i=0; i<K*nLen; i++)//先把buffer数组置0
{
buffer[i] = 0;
}
fseek(fp, 0, SEEK_SET); //指向文件开始
fread(buffer, 1, nSize, fp); //复制文件到buffer数组
fclose(fp);
byte *p = buffer; //用来遍历buffer数组
byte** Buf; //文件数据存入二维数组中K*nLen
Buf = new byte*[K]; //把buffer数组存入二维数组Buf
for (i = 0; i < K; i++){
Buf[i] = new byte[nLen];
}
byte *p = buffer;
for (i = 0; i < K; i++){
for (j = 0; j < nLen; j++){
Buf[i][j] = *p;
p++;
}
}
delete[] buffer; //使用new数组,使用完记得释放空间
3、获取随机编码矩阵
byte** encodeMatrix; //编码矩阵N*K
encodeMatrix = new byte*[N];
for (i = 0; i < N; i++){
encodeMatrix[i] = new byte[K];
}
srand((unsigned)time(NULL));
for (i = 0; i < N; i++) //生成随机矩阵
{
for (j = 0; j < K; j++)
{
encodeMatrix[i][j] = rand() % 256; //因为是在GF(256) 的域上进行的运算
}
}
4、编码操作
byte** matrix1; //用来存储编码结果N*nLen的编码结果
matrix1 = Multiply(encodeMatrix, Buf, N, K, nLen);
编码就是用编码矩阵乘以文件数据矩阵,矩阵相乘和矩阵求逆的函数,在后面给出。 5、把K值、编码矩阵与编码结果拼接起来组成一个矩阵,在分行写入N个encodeFile文件
byte** Mat; //把编码矩阵与编码结果组成一个矩阵,这是一个N*(1+K+nLen)的矩阵
Mat = new byte*[N];
for (i = 0; i < N; i++){
Mat[i] = new byte[1 + K + nLen];
}
for (i = 0; i < N; i++){ //第0列全为K
Mat[i][0] = K;
}
for (i = 0; i < N; i++){ //1到K列为编码矩阵encodeMatrix
for (j = 1; j <= K; j++){
Mat[i][j] = codeMatrix[i][j - 1];
}
}
for (i = 0; i < N; i++){ //K+1到K+nLen为编码结果矩阵matrix1
for (j = K + 1; j <= K + nLen; j++){
Mat[i][j] = matrix1[i][j - K - 1];
}
}
//把矩阵matrix2按行分开存入N个codeFile文件
FILE *fpCd;
char filename[32];
for (i = 1; i <= N; i++)
{
_snprintf_s(filename, 32, "codeFile%d.", i); //创建文件,为文件命名
strcat_s(filename, T2A(g_extName.GetBuffer())); //连接上扩展名
fopen_s(&fpCd,filename, "wb");
fwrite(Mat[i - 1], 1, 1 + K + nLen, fpCd); //写入
fclose(fpCd);
}
6、文件多选窗口的实现
//获取当前工作路径
TCHAR szPath[MAX_PATH];
GetModuleFileName(NULL, szPath, MAX_PATH);
CString PathName(szPath);
CString PROGRAM_PATH = PathName.Left(PathName.ReverseFind(_T('\\')) + 1);
//多选文件
size_t index;
CString cstrsucstring;
CFileDialog filedlg(TRUE, NULL, NULL, OFN_HIDEREADONLY | OFN_OVERWRITEPROMPT | OFN_ALLOWMULTISELECT, _T("Code Files(*.nc)|*.nc||"));
TCHAR *pBuffer = new TCHAR[MAX_PATH * 100]; //最多允许同时打开100个文件
filedlg.m_ofn.lpstrInitialDir = PROGRAM_PATH; //设置打开选择框时的目录
filedlg.m_ofn.lpstrFile = pBuffer;
filedlg.m_ofn.nMaxFile = MAX_PATH * 100;
filedlg.m_ofn.lpstrFile[0] = '\0';
int count = 0; //count用来记录选择了几个文件
CString* cstrfilepath = new CString[100]; //文件名存入cstrfilepath数组
if (filedlg.DoModal() == IDOK)
{
POSITION pos = filedlg.GetStartPosition();
while (pos != NULL)
{
cstrfilepath[count] = _T("");
cstrfilepath[count++] = filedlg.GetNextPathName(pos); //取得所选文件路径
}
}
if (count == 0){
Step_info += "You don't have a choice of files.";
return;
}
char** fileName = new char*[count]; //分离出不含路径的文件名
for (int i = 0; i < count; i++){ //放入fileName数组以供取用
fileName[i] = new char[32];
}
USES_CONVERSION;
int i,j;
for (i = 0; i < count; i++){
CString fn = cstrfilepath[i].Right(cstrfilepath[i].GetLength() - cstrfilepath[i].ReverseFind('\\') - 1);
char* ch = T2A(fn);
for (j = 0; *ch != '\0'; ch++, j++){
fileName[i][j] = *ch;
}
fileName[i][j] = '\0';
}
delete[] pBuffer;
delete[] cstrfilepath;
7、再编码时对文件内容的分离
byte** Buffer; //把编码后文件读入数组
Buffer = new byte*[count]; //Buffer矩阵用于选择文件的读入与写回
for (i = 0; i < count; i++){
Buffer[i] = new byte[length];
}
FILE* fpCd;
for (i = 0; i < count; i++){
fopen_s(&fpCd, fileName[i], "rb");
fread(Buffer[i], 1, length, fpCd);
fclose(fpCd);
}
byte** matrix1; //取出编码矩阵和编码后的数据
matrix1 = new byte*[count];
for (i = 0; i < count; i++){
matrix1[i] = new byte[length - 1];
}
for (i = 0; i < count; i++){
for (j = 0; j < length - 1; j++){
matrix1[i][j] = Buffer[i][j + 1]; //Buffer数组的第0列存的是文件编码前平均//分成的个数,这一列不读出
}
}
接下来就是用随机生成的再编码矩阵(num×num)与从codeFile文件取出的数据矩阵相乘,进行再编码。然后把再编码结果写回Buffer数组,再写回文件,并把文件重命名为re_encodeFile,这些操作与编码时相同。 8、解码过程。 先是打开文件选择界面多选文件,实现和再编码多选文件时操作一样。
//从文件中分离出编码矩阵和编码后的数据
byte** MAT; //用来存放nPart个解码文件,是一个nPart*nLength的矩阵
MAT = new byte*[nPart];
for (i = 0; i < nPart; i++){
MAT[i] = new byte[nLength];
}
FILE *fpCd;
for (i = 0; i < nPart; i++)
{
fopen_s(&fpCd, fileName[i], "rb");
fread(MAT[i], 1, nLength, fpCd);
fclose(fpCd);
}
//从数组中分离编码矩阵和编码结果
byte** encodeMAT; //编码矩阵为nPart*nPart矩阵
encodeMAT = new byte*[nPart];
for (i = 0; i < nPart; i++){
encodeMAT [i] = new byte[nPart];
}
for (i = 0; i < nPart; i++){
for (j = 0; j < nPart; j++){
encodeMAT [i][j] = MAT[i][j + 1];
}
}
byte** MAT1; //编码结果为nPart*(nLength-nPart-1)矩阵
MAT1 = new byte*[nPart];
for (i = 0; i < nPart; i++)
{
MAT1[i] = new byte[nLength - nPart - 1];
}
for (i = 0; i < nPart; i++)
{
for (j = 0; j < nLength - nPart - 1; j++)
{
MAT1[i][j] = MAT[i][j + 1 + nPart];
}
}
//对编码矩阵求逆
byte** IvEncodeMAT; //编码矩阵的逆矩阵
IvEncodeMAT = Inverse(encodeMAT, nPart);
//解码MAT3*MAT2用MAT4来接收结果
byte** dataMat;
dataMat = Multiply(IvEncodeMAT, MAT1, nPart, nPart, nLength - nPart - 1);
//把dataMat写回文件
str=fileName[0]; //编码后的文件名如*.jpg.nc,从中提取出jpg
CString ext1 = str.Right(str.GetLength() - str.Find('.') - 1); //如jpg.nc
CString extName = ext1.Left(ext1.GetLength() - ext1.Find('.')); //如jpg
CString fn ("recovery.");
fn += extName;
FILE* fp1;
fopen_s(&fp1,T2A(fn),"wb");
for (i = 0; i < nPart; i++)
{
fwrite(dataMat[i], 1, nLength - nPart - 1, fp1); //写入恢复文件
}
fclose(fp1);
整个程序的核心操作有文件的选择、写入和读出,矩阵的乘法和求逆。
文件的写入和读出一定注意要使用二进制方式操作,还需要把gf文件夹复制到项目的资源目录下,程序的头文件包含gf.c。
矩阵的操作有4个地方需要注意: 1、把文件平均分成K份时,不足的部分补0。 2、编码部分最后写入文件的矩阵由三部分组成:0列存放的是K值;1到K列存放的编码矩阵,最后一部分为编码结果。 3、再编码是对文件中存放的编码矩阵和编码结果部分进行操作,不包括前面的K值。 4、new数组一定要用delete释放。当然矩阵的相乘和求逆操作都是在有限域GF(256)上进行,具体的代码后面给出。
下面给出矩阵相乘和矩阵求逆的函数,比较长,所以就写在最后了。 矩阵相乘的函数:
byte** CNetworkCodingDlg::Multiply(byte** matA, byte** matB, int nRow, int n, int nCol)
{ //nRow*n的矩阵matA乘以n*nCol的矩阵matB,返回乘积矩阵
int i, j, k;
int temp;
gf_init(8, 0x00000187); //初始化域
byte** Mat; //用来存储矩阵相乘结果 (nRow*nCol)
Mat = new byte*[nRow];
for (i = 0; i < nRow; i++){
Mat[i] = new byte[nCol];
}
for (i = 0; i < nRow; i++){ //两矩阵相乘
for (j = 0; j < nCol; j++){
temp = 0;
for (k = 0; k < n; k++){
temp = gf_add(temp, gf_mul(matA[i][k], matB[k][j]));
}
Mat[i][j] = temp;
}
}
gf_uninit();
return Mat;
}
矩阵求逆的函数:
byte** CNetworkCodingDlg::Inverse(byte** G, int n) //n为矩阵的维数
{
//求秩
int i;
int nRow = n;
int nCol = n;
gf_init(8, 0x00000187);
byte **M = new byte*[nRow];
for (int j = 0; j<nRow; j++)
{
M[j] = new byte[nCol];
}
for (int i = 0; i<nRow; i++)
{
for (int j = 0; j<nCol; j++)
{
M[i][j] = *(*(G + i) + j);
}
}
for (int i = 0; i<nRow; i++)
{
for (int j = 0; j<nCol; j++)
{
TRACE("%d\t", M[i][j]);
}
TRACE("\n");
}
TRACE("\n");
// Define a variable to record the position of the main element.
int yPos = 0;
for (int i = 0; i<nRow; i++)
{
// Find the main element which must be non-zero.
bool bFind = false;
for (int x = yPos; x<nCol; x++)
{
for (int k = i; k<nRow; k++)
{
if (M[k][x] != 0)
{
// Exchange the two vectors.
for (int x = 0; x<nCol; x++)
{
byte nVal = M[i][x];
M[i][x] = M[k][x];
M[k][x] = nVal;
} // We have exchanged the two vectors.
bFind = true;
break;
}
}
if (bFind == true)
{
yPos = x;
break;
}
}
for (int j = i + 1; j<nRow; j++)
{
// Now, the main element must be nonsingular.
byte temp = gf_div(M[j][yPos], M[i][yPos]);
for (int z = 0; z<nCol; z++)
{
M[j][z] = gf_add(M[j][z], gf_mul(temp, M[i][z]));
}
}
//
yPos++;
}
// The matrix becomes a scalar matrix. we need to make more elements become 0 with elementary transformations.
yPos = 0;
for (int i = 1; i<nRow; i++)
{
for (int j = 0; j<nCol; j++)
{
if (M[i][j] != 0)
{
// the main element is found.
yPos = j;
break;
}
}
for (int k = 0; k<i; k++)
{
byte temp = gf_div(M[k][yPos], M[i][yPos]);
for (int z = 0; z<nCol; z++)
{
M[k][z] = gf_add(M[k][z], gf_mul(temp, M[i][z]));
}
}
}
int nRank = 0;
// Get the rank.
for (int i = 0; i<nRow; i++)
{
int nNonzero = 0;
for (int j = 0; j<nCol; j++)
{
if (M[i][j] != 0)
{
nNonzero++;
}
}
// If there is only one nonzero element in the new matrix, it is concluded an original packet is leaked.
if (nNonzero > 0)
{
// Leaked.
nRank++;
}
}
for (int i = 0; i<nRow; i++)
{
delete[] M[i];
}
delete[] M;
//求逆
int bRet = nRank;
if (bRet != nRow)
{
return NULL;
}
/************************************************************************/
/* Start to get the inverse matrix! */
/************************************************************************/
byte **N = new byte*[nCol];
for (int j = 0; j<nCol; j++)
{
N[j] = new byte[2 * nCol];
}
for (i = 0; i<nCol; i++)
{
for (int j = 0; j<nCol; j++)
{
N[i][j] = G[i][j];
TRACE("%d\t", N[i][j]);
}
for (int j = nCol; j<2 * nCol; j++)
{
if (i == j - nCol)
{
N[i][j] = 1;
}
else
{
N[i][j] = 0;
}
TRACE("%d\t", N[i][j]);
}
TRACE("\n");
}
/************************************************************************/
/* Step 1. Change to a lower triangle matrix. */
/************************************************************************/
for (i = 0; i<nCol; i++)
{
// There must exist a non-zero mainelement.
TRACE("*********\n");
if (N[i][i] == 0)
{
// Record this line.
byte temp[200] = { 0 };
for (int k = 0; k<2 * nCol; k++)
{
temp[k] = N[i][k];
}
// Exchange
int nRow = nCol; // They are the same in essensial.
for (int z = i + 1; z<nRow; z++)
{
if (N[z][i] != 0)
{
for (int x = 0; x<2 * nCol; x++)
{
N[i][x] = N[z][x];
N[z][x] = temp[x];
}
break;
}
}
}
for (int j = i + 1; j<nCol; j++)
{
// Now, the main element must be nonsingular.
byte temp = gf_div(N[j][i], N[i][i]);
for (int z = 0; z<2 * nCol; z++)
{
N[j][z] = gf_add(N[j][z], gf_mul(temp, N[i][z]));
}
}
}
/************************************************************************/
/* Step 2. Only the elements on the diagonal are non-zero. */
/************************************************************************/
for (i = 1; i<nCol; i++)
{
for (int k = 0; k<i; k++)
{
byte temp = gf_div(N[k][i], N[i][i]);
for (int z = 0; z<2 * nCol; z++)
{
N[k][z] = gf_add(N[k][z], gf_mul(temp, N[i][z]));
}
}
}
/************************************************************************/
/* Step 3. The elements on the diagonal are 1. */
/************************************************************************/
for (i = 0; i<nCol; i++)
{
if (N[i][i] != 1)
{
byte temp = N[i][i];
for (int z = 0; z<2 * nCol; z++)
{
N[i][z] = gf_div(N[i][z], temp);
}
}
}
/************************************************************************/
/* Get the new matrix. */
/************************************************************************/
byte **CM = new byte*[nCol];
for (int j = 0; j<nCol; j++)
{
CM[j] = new byte[nCol];
}
for (i = 0; i<nCol; i++)
{
for (int j = 0; j<nCol; j++)
{
CM[i][j] = N[i][j + nCol];
}
}
// Clean the memory.
gf_uninit();
for (i = 0; i<nCol; i++)
{
delete[] N[i];
}
delete N;
return CM;
}